Han Liu 七 and Mathieu Bauchy1
1 University of California, Los Angeles, California, 90095, USA
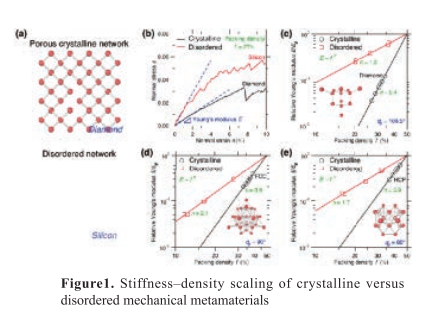
EXTENDED ABSTRACT: The evolution of the Young's modulus (E) of disordered materials (e.g., glasses) as a function of their density (p) is typically governed by some scaling laws E 〜pn, wherein less efficiently packed structures (i.e., lower p) are also less stiff (lower E). The drop in stiffiiess upon decreasing density is governed by the scaling exponent n, wherein larger scaling exponent results in a more pronounced drop in stiffiiess. Here, by combining high-throughput molecular dynamics (MD) simulations and Bayesian-optimization- based machine learning (ML), we predict the existence of a “stretching-dominated',family of disordered networks exhibiting minimum scaling exponent. This paves the way toward the design of new ultralight, yet ultrastiff non-crystalline phases.
KEYWORDS: Disordered Metamaterials, Stiffiiess, Molecular Dynamics, Machine Learning

Han LIU is a materials physicist who is combining computational simulations and machine learning techniques to accelerate the design of disordered materials, including glassy materials, porous materials, and mechanical metamaterials. He obtained his Ph.D. from the Department of Civil and Environmental Engineering at University of California, Los Angeles (UCLA) in 2021, and concurrently obtained a master's degree from the Department of Electrical and Computer Engineering at UCLA in 2020. Prior to UCLA, he obtained his bachelor's and master5s degrees from the College of Polymer Science and Engineering at Sichuan University (SCU, CHINA). Since 2022, he continued to work as a Postdoc at UCLA and now join SCU as a faculty. So far, he has published 25 scientific papers, including 15 first-author publications. His present research interest lies in the intersection between machine learning and computational materials.
By developing the cutting-edge techniques and theories of artificial intelligence (Al), he systematically investigates the AI-
computing methodologies for materials modeling and inverse design and, ultimately, aims to build an advanced Al-computing
platform for mechanical metamaterials (and materials design in general).