Ben Xu
Graduate School of China Academy of Engineering Physics
Magnetic ordering plays a pivotal role in determining the macroscopic properties of various materials, ranging from spintronic
devices to non-magnetic materials such as ternary lithium battery components, uranium oxide materials, and austenitic steels. The complexity of research in this field arises from the intricate interplay between atomic structure and magnetic ordering, further compounded by the influence of temperature and external fields on the system's ground state and evolutionary mechanisms. A significant challenge within this domain is the requirement for high energy accuracy and resolution, capable of discerning local atomic environment energy variations on the order of 10 me V. Addressing these challenges, we introduce an atomic-scale lattice-spin dynamics computational approach that is particularly well-suited for such investigations. The crux of this approach
lies in the precise characterization of the lattice spin interaction. We report the development of an innovative first-principles method for magnetic excited states-DeltaSPIN-which incorporates a vectorized local confinement field. This method iteratively refines the self-consistency between the confinement field and electron distribution,successfully resolving the longstanding issue of magnetic confinement accuracy in first-principles calculations, now implemented within the ABACUS open-source software suite. Utilizing DeltaSPIN, we achieve meticulous calculations of system energy, atomic forces, and magnetic torques across varying lattice and magnetic states. These calculations serve as inputs to a deep learning network, synergizing with a pseudo-atomic methodology for lattice-magnetic moment characterization to formulate the DeePSPIN method. DeePSPIN allows for the development of lattice magnetic moment potential functions with first-principles accuracy, ensuring precision in syst叩 energy, atomic forces, and magnetic moments in atomic-scale simulations气uantified to 0.1 meV/atom, 0.01 meV/A, and 0.1 meV/µB. For systems exhibiting coexisting magnetic and lattice features, traditional computational methods necessitate separate and iterative optimization of each subsystem to deduce the ground state. To overcome this limitation, we have conceived a synergistic conjugate gradient method that facilitates simultaneous optimization of both systems, thereby expediting the discovery of states in high-dimensional systems.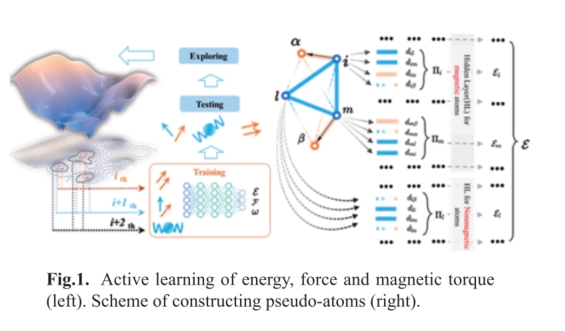
Keywords: Magnetic materials, Potential, atomic simulation